La Théorie des Electrons

MESSIEURS,

Dans les dernières années, les physiciens ont développé une activité aussi grande que féconde en résultats importants. Les recherches expérimentales sur les phénomènes qui se produisent dans la décharge électrique, la découverte de nouveaux rapports entre la lumière et le magnétisme, les remarquables propriétés du radium et des substances radioactives en général ont eu pour conséquence la formation d'une branche intéressante de a physique et d'une nouvelle théorie. Cette théorie non seulement rend compte de tous les faits observés, mais en même temps, modifie complètement les idées sur les phénomènes physiques en général et sur la structure de la matière.

En 1896, le physicien néerlandais Zeeman découvrait le phénomène intéressant que la lumière émise par une flamme change de couleur lorsque cette flamme est placée entre les pôles d'un aimant. Précisons. Le spectre d'un gaz lumineux se compose de raies; la vapeur de cadmium contient par exemple une raie verte. Lorsque cette flamme est placée dans un champ magnétique, nous voyons, en la

regardant dans une direction perpendiculaire à la droite qui relie les pôles de l'aimant, apparaître deux nouvelles raies vertes, à gauche et à droite de la première. Une partie de la lumière émise s'est donc transformée dans un vert un peu plus foncé; une seconde partie, par contre, est devenue plus claire, tandis qu'une troisième partie enfin na pas changé. Certes, les distances des trois raies obtenues sont extrêmement petites et il faut une bien grande habileté expérimentale pour les mettre en évidence, mais si petites qu'elles soient, le phénomène observé par Zeeman avait une grande importance, parce qu'il venait confirmer d'une manière éclatante, au moins quant à une de ses conséquences, la théorie des électrons formulée quelques années auparavant par M. Lorentz, professeur à Leyde.

Cette théorie ne rendait pas seulement compte du phénomène, dont nous venons de décrire une des formes les plus simples, elle permettait encore de prévoir que la première et la troisième des raies obtenues devaient être complètement polarisées circulairement dans des sens opposés. La confirmation éclatante de ce résultat théorique par l'expérience attira définitivement l'attention du monde des physiciens sur l'hypothèse de Lorentz. Dans une période de dix ans à peine, cette théorie n'a pas seulement permis — grâce aux travaux mathématiques de son inventeur, de Drude, d'Abraham, de Riecke, J.-J. Thomson, etc., grâce encore aux expériences aussi délicates qu'ingénieuses de Zeeman, Townsend, Kaufmann, des deux Wilson, Rutherford, Soddy, Ramsay et de beaucoup d'autres — de pénétrer plus profondément dans les phénomènes physiques et météorologiques, elle est encore devenue un facteur d'une haute importance dans la mécanique aussi bien que dans la chimie. Elle mérite donc, à tous égards, d'être connue. Avant cependant

de dire aussi brièvement et aussi simplement que possible en quoi elle consiste, il ne sera pas inutile de faire remarquer d'une part, que le temps ne me permettra pas de vous parler des expériences si multipliées et si variées qui sont venues la confirmer et, d'autre part, que dans cette théorie en plein développement il y a encore bien des points à éclaircir.

Pour arriver à l'idée de l'électron, supposons que dans l'éther une sphère creuse conductrice ait une certaine charge électrique positive, tandis qu'à quelque distance une sphère pareille possède une charge égale à celle de la première, mais de signe contraire. La seconde, étant attirée par la première, possédera par rapport à elle une certaine énergie potentielle qui, d'après Clerk Maxwell, doit avoir son siège dans l'éther environnant; cette énergie, emmagasinée dans l'éther, ne dépend nullement de l'épaisseur des parois sphériques. Nous pouvons donc théoriquement diminuer indéfiniment cette épaisseur, c'est-à-dire rendre la masse des sphères absolument négligeable, sans changer quoi que ce soit à l'énergie électrique qu'elles représentent. Jusqu'ici les deux sphères étant en repos, il n'y a dans l'éther environnant aucune action magnétique. Celle-ci ne se manifeste que lorsqu'une des sphères est mise en mouvement, et, dans ce cas, l'énergie emmagasinée dans le milieu environnant n'est plus électrique, elle est devenue électromagnétique, et sa grandeur varie avec la position et la vitesse de la sphère en mouvement. Or, un changement de la vitesse ne peut se faire remarquer à une certaine distance qu'après un certain temps, d'autant plus grand que la distance est plus considérable. Maxwell a démontré théoriquement et la preuve expérimentale a été fournie par Hertz, que la vitesse avec laquelle une pareille perturbation se propage dans l'éther est égale à celle de la lumière, de sorte que le mouvement d'une

sphère électrisée produit une perturbation dans l'éther à une distance de 3oo Km. après 1/1000 de seconde. Si nous donnons à la sphère un mouvement régulier de va-et-vient, un mouvement périodique, celui-ci provoquera dans l'éther des changements réguliers ayant la même période, c'est-à-dire des ondes, qui se propagent avec la vitesse de la lumière. Ces ondes ne sont, en somme, autre chose que celles, qu'on emploie dans la télégraphie sans fil. Si l'action n'était pas aussi faible, une sphère électrisée exécutant des oscillations régulières pourrait donc remplacer l'excitateur dans les appareils de Marconi. Les ondes produites ont une longueur énorme, mais, à part cela, elles ne diffèrent pas — nous le savons par la théorie de Maxwell et les expériences de Hertz — des ondes lumineuses 1. Il suffirait donc de faire le diamètre de la sphère électrisée extrêmement petit et de rendre la durée de son oscillation très courte, pour que la perturbation périodique produite par son mouvement oscillatoire dans l'éther ait tous les caractères d'un rayon lumineux.

Lorentz, continuant l'oeuvre de Maxwell, voit donc dans chaque source lumineuse des petites sphères électrisées ayant une masse, dans le sens ordinaire du mot, négligeable et exécutant des oscillations autour d'une certaine position d'équilibre. Ces petits corps, ayant tous la même charge positive ou négative, ne sont autre chose que les électrons. D'après les calculs de Max Abraham, leur diamètre est de quelques billionièmes de millimètre, tandis que par des mesures extrêmement variées, on a toujours trouvé la même valeur pour le rapport entre leur charge et leur masse (apparente) ^2. Chaque atome d'un corps contient au moins un électron positif et un électron négatif. Dans certaines substances, particulièrement dans les métaux, l'électron négatif se sépare très facilement de

l'atome qui, restant lié à l'autre électron, possédera, dans ce cas, une charge positive. Dans d'autres corps, par contre, l'électron négatif, quoique possédant dans l'atome une certaine liberté de mouvement, ne peut s'en séparer qu'au prix d'un très grand effort extérieur. Ce sont là les corps non-conducteurs ou diélectriques. Nous allons voir comment cette différence dans la mobilité des électrons négatifs explique par exemple la grande facilité avec laquelle la chaleur aussi bien que l'électricité se propagent dans les métaux. Les électrons négatifs libérés dans un métal, se meuvent parmi les atomes restés positifs ou neutres comme les molécules d'un gaz enfermé dans une enveloppe, c'est-à-dire d'une manière absolument désordonnée. Si, dans une partie du métal, la température est plus élevée que dans les parties avoisinantes, il en sera de même pour la vitesse moyenne des électrons libérés. Grâce à leur extrême mobilité, ceux qui sont doués de grande vitesse passeront dans les couches voisines et seront remplacés par d'autres dont la vitesse moyenne est inférieure. De cette manière, les différences des vitesses s'effacent et, après peu de temps, la vitesse moyenne des électrons, comme la température, seront les mêmes partout. Il est cependant à remarquer que les électrons des deux espèces sont toujours en nombre égal dans chaque partie du métal. On ne constate donc extérieurement aucune action électrique, le phénomène est de nature purement thermique.

Il en est autrement lorsque le mouvement des électrons n'est plus désordonné, c'est-à-dire lorsqu'une cause quel-conque, qu'on nomme ordinairement une force électromotrice, et qu'on pourrait aussi appeler électronomotrice, pousse les électrons dans une direction déterminée 3. Dans ce cas, il se produit dans le métal, par les électrons même, un transport d'électricité, c'est-à-dire un courant

électrique qui est toujours accompagné d'un dégagement de chaleur plus ou moins grand. Comment la théorie des électrons rend-elle compte de cette chaleur qui fait briller nos lampes électriques? D'une manière bien simple. Les électrons, poussés par la force électromotrice constante qui. donne le courant, acquerraient une vitesse croissante s'ils n'éprouvaient aucune résistance de la part des atomes du métal. A cause de cette résistance, la vitesse dans la direction du courant reste sensiblement la même, tandis que le mouvement désordonné des électrons et des atomes, c'est-à-dire le mouvement qui correspond à la température, augmente. Il serait intéressant de parler encore sur la manière dont la théorie électronique envisage le transport de l'électricité dans un électrolyte 4 et dans un gaz et de dire un mot sur la façon dont elle explique si simplement l'induction et tous ces phénomènes électriques et électrooptiques, qui portent les noms de Peltier, Thomson, Hall 5, Kerr, Zeeman, etc. Il me tarde cependant d'arriver à un phénomène connu depuis longtemps et qui a une grande importance depuis les découvertes si remarquables. sur le radium et la radioactivité faites par M. Becquerel, M. et Mme Curie et bien d'autres. Je veux dire les rayons. cathodiques.

Il y a un instant, je vous disais que les électrons négatifs libres qui se trouvent dans un métal acquerraient, sous l'influence d'une force électromotrice constante, une vitesse croissante s'ils n'étaient arrêtés constamment par les atomes ou par les atomes diminués de l'électron négatif du métal. Supposons cependant que le bout du métal vers lequel tendent les électrons négatifs — on appelle ce bout la cathode — soit enfermé dans une ampoule absolument vide; dans ce cas, les électrons en arrivant là n'éprouveront plus aucune résistance et ils seront lancés dans l'espace vide avec des vitesses qui

dépendent de la force électromotrice. Ce sont ces électrons en mouvement rectiligne, partant normalement de la cathode, qui forment les rayons cathodiques. Ce sont eux qui, arrivant sur la paroi opposée dé l'ampoule, font fluorescer le verre; ce sont eux encore qui y font naître les rayons si mystérieux que, depuis dix ans, nous connaissons sous le nom de rayons X.

Les rayons cathodiques peuvent se former de bien d'autres manières encore. Ainsi l'on en obtient de très faibles, il est vrai, lorsqu'on fait tomber de la lumière ultraviolette sur un métal possédant une charge négative. De même on en produit en chauffant à blanc des fils de métal. Mais ce sont surtout certaines substances, les unes connues depuis longtemps, comme l'uranium et le thorium, d'autres connues seulement depuis quelques années comme le radium, le polonium et l'actinium, qui toujours et dans toutes leurs combinaisons émettent ces processions d'électrons, se mouvant plus ou moins vite, qui constituent les rayons cathodiques. C'est surtout le radium, cette substance si remarquable, que la science doit à l'ingéniosité, à la patience et à l'habileté expérimentale de M. et M me Curie, qui émet ces rayons le plus abondamment.

On pouvait présumer que nulle part les propriétés des électrons négatifs ne pourraient. être étudiées d'une manière plus simple que dans ces rayons cathodiques qui les contiennent à l'état libre. Les espérances des physiciens se sont pleinement réalisées. Par une série d'expériences sur des rayons cathodiques de toute provenance, on est arrivé au résultat que la charge des électrons, quelle que soit leur origine, est partout et toujours la même. Les électrons sont donc comme les atomes indivisibles et invariables de l'électricité. Comme il était facile de le prévoir, leur vitesse varie entre de très grandes limites. Il y a cependant un troisième facteur, qui joue un rôle

considérable, c'est la masse des électrons. Ici les expériences celles de Kaufmann surtout — ont conduit à un résultat tout à fait imprévu et surprenant. C'est ce résultat qui, pour ui grand nombre de physiciens, a modifié complètement les idées aussi bien sur la structure de la matière que sur les bases même de la mécanique et de la chimie. Le temps restreint ne m'a pas permis de vous parler jusqu'ici des expériences qui ont fourni les résultats, dont je vous ai donné un aperçu.

Il faut cependant que je fasse une exception pour celles de Kaufmann, à cause de leur très grande importance théorique. Supposons donc qu'on veuille augmenter d'une unité la vitesse d'un corps. Pour cela, il faut une force qui ne dépend que de la masse du corps lorsque celui-ci est libre; mais si ce corps doit se mouvoir dans un liquide, qui participe plus ou moins à son mouvement, il faudra, pour obtenir le même effet, évidemment une force plus grande. On pourrait donc dire que, grâce à l'influence du liquide, la masse du corps a augmenté. Ceci n'est qu'apparent. La masse du corps n'a pas changé; seulement il est venu s'ajouter une masse apparente due au liquide qui participe à son mouvement. On a quelque chose d'analogue dans le mouvement d'un électron. Il est impossible de changer sa vitesse sans changer en même temps l'état électromagnétique de l'éther environnant. Sa masse totale doit donc aussi se composer de deux parties: la première étant sa véritable masse à lui, la seconde étant une masse apparente due à l'influence de l'éther. Cette dernière, d'après les calculs de Max Abraham, augmente avec la vitesse; il en est donc de même pour la masse totale. Cela étant, parlons maintenant des expériences de Kaufmann 6. Le rayon cathodique n'a pas seulement le pouvoir de rendre fluorescentes certaines substances; il impressionne aussi la plaque photographique. Composé

de petits corpuscules électrisés, comme il l'est, il est évident qu'une force électrique étrangère, perpendiculaire à sa direction, lui donnera une certaine déviation. Supposons que cette déviation aille de gauche à droite et qu'on fasse en même temps agir sur les électrons une force magnétique. Celle-ci aussi provoquera une déviation, car les électrons en mouvement constituent un courant. Il est facile de faire en sorte que cette déviation-là aille de haut en bas. Au lieu donc d'impressionner le point de la plaque photographique comme auparavant. le rayon cathodique agira maintenant sur un point qui est situé un peu plus haut et un peu plus à droite. Si nous avons affaire à un rayon cathodique dans lequel les électrons se meuvent avec une vitesse plus grande ou plus petite, la déviation obtenue sera plus petite ou plus grande et ce rayon-là impressionnera un autre point de la plaque photographique. Le radium émet des rayons cathodiques de vitesses variant entre de grandes limites; ils impressionneront par conséquent la plaque photographique dans une série de points qui forment ensemble une courbe. C'est la forme de cette courbe qui a permis à Kaufmann de formuler une conclusion très importante. Il trouvait, en effet, que la masse totale augmente avec la vitesse, comme les calculs de Max Abraham le faisaient prévoir, mais il trouvait encore, en étudiant la courbe obtenue, que la masse totale augmente avec la vitesse dans la même proportion que la masse apparente. Il s'ensuit — et c'est là le point capital de ces recherches — que la masse réelle de l'électron est nulle. Ce petit corps électrisé n'a donc qu'une masse apparente due à l'énergie électromagnétique de l'éther et celle-ci croît avec la vitesse. Le calcul montre cependant qu'elle ne varie considérablement que lorsque la vitesse est comparable à celle de la lumière. Pour toutes les vitesses modérées, elle est pratiquement

constante et d'après les expériences très variées qu'on a faites., elle est environ 1/2000 de celle du plus petit des atomes. Les électrons présentent donc trois propriétés bien singulières: 1° leur masse est seulement apparente ou de nature électromagnétique; 2° cette masse n'est pas invariable: elle croît avec la vitesse et 3° elle est pour. des vitesses modérées beaucoup plus petite que celle du plus petit des atomes.

Nous allons voir, dans un instant l'importance de ces faits dans la nouvelle théorie sur la structure de la matière. Mais disons d'abord un mot sur les électrons positifs. Ceux-là, nous le savons, ne se séparent que très difficilement de l'atome et leur étude est, de ce fait, beaucoup moins simple que celle des électrons négatifs. Cependant nous pouvons présumer que, pour eux aussi, Ia masse est de nature électromagnétique et fonction de la vitesse.

On pourrait s'en tenir là et admettre à côté des électrons sans masse réelle la possibilité de la matière ordinaire. Beaucoup de physiciens cependant sont allés plus loin. Ils se sont demandés: Si la masse des électrons est seulement apparente, en est-il peutêtre de même pour toutes les masses? ou encore: N'est-il pas possible que les atomes ne soient que des agglomérations d'électrons positifs et négatifs?

II faut dire qu'en donnant à ces questions une réponse affirmative, ils faisaient une hypothèse qui n'était pas la seule possible. Cependant les conséquences de cette nouvelle hypothèse, qui est venue se greffer sur celle de Lorentz, sont si intéressantes, elles rendent si bien compte des phénomènes mystérieux de la radioactivité découverts par Becquerel et Curie, elles nous ouvrent un si vaste horizon sur les phénomènes chimiques que nous allons les examiner d'un peu plus près.

D'après cette hypothèse, les combinaisons chimiques ne contiennent plus qu'éther et électrons, et comme la masse de ces derniers est apparente ou de nature électromagnétique, il doit en être de même pour les atomes et les molécules qui constituent les corps. Enfin, et ceci est très grave: cette masse apparente des corps n'est plus invariable, elle est croissante avec la vitesse comme celle des électrons. Il est vrai que, pour des vitesses ordinaires, cette variation de la masse est absolument négligeable; elle ne devient importante que lorsque ces vitesses s'approchent de celle de la lumière, mais il n'en est pas moins vrai qu'en supposant la masse des corps fonction de la vitesse, on rend fort peu solide un des piliers principaux qui soutiennent l'édifice de la mécanique analytique. Ce n'est d'ailleurs pas le seul qu'on ait attaqué. La thermodynamique aussi a sapé un peu les fondements de cet édifice. Si l'on n'est pas électroniste à outrance, si l'on s'en tient à la simple hypothèse de Lorentz, qui, par toutes les recherches qu'on y a consacrées, est devenue si hautement plausible, les conflits ne manquent pas avec cette mécanique qui, il n'y a pas bien longtemps encore — fut jugée assez parfaite pour expliquer tous les phénomènes organiques et vitaux aussi bien qu'inorganiques. Ainsi on arrive parfois, dans la théorie des électrons, à des actions pour lesquelles on cherchera vainement des réactions égales, qui donc, étant contraires au principe de l'égalité simultanée entre action et réaction, sont inadmissibles dans la mécanique classique. La chose est d'ailleurs facile à comprendre si l'on retient que les électrons agissent les uns sur les autres par l'intermédiaire de l'éther. Une perturbation produite par un premier électron atteint un second et modifie sa vitesse seulement après un certain temps, qui est d'autant plus grand que la distance des deux électrons est plus considérable. Pour tout observateur

qui ne tient compte que des mouvements de la matière, c'est-à-dire des électrons, la réaction exercée par le second électron viendra pius tard que l'action du premier et ceci — nous le savons — est déjà en contradiction avec le principe de Newton d'après lequel la compensation des deux est simultanée.

Maxwell d'ailleurs, il y a quarante ans, était déjà arrivé à des conclusions analogues. D'après sa théorie --- et celle de Lorentz n'en est que la continuation — la lumière réfléchie par un miroir doit exercer sur ce miroir une certaine pression, dont il était en état de calculer la valeur extrêmement petite 7. Dans ces dernières années seulement, Lebedew d'une part, Nichols et Hull d'autre part, ont pu vérifier, par l'expérience, le résultat théorique de Maxwell. Ils n'ont pas seulement trouvé que la pression existe, mais qu'elle a exactement la valeur prédite par Maxwell. Dans ce cas, comme dans celui que nous venons d'exposer, l'action part de la source lumineuse, la réaction du miroir ne vient que plus tard, lorsque la lumière a parcouru la distance qui les sépare.

Un autre principe fondamental de la mécanique classique, celui de l'inertie est également ébranlé par la théorie des électrons. En effet, Sommerfeld a démontré qu'il y a un cas où la vitesse varie sans intervention d'une force. Lorsque la vitesse d'un électron est supérieure à celle de la lumière, elle doit diminuer, même sans l'action d'une cause matérielle extérieure.

Il ressort de tout cela que, pour les électronistes, les principes de la mécanique classique, s'ils ne sont pas inexacts, sont au moins incomplets, et s'il est certain qu'une partie de l'édifice puisse être sauvée et conservée, il n'en est pas moins vrai que les fondements, demandent impérieusement à être consolidés et élargis.

Aussi longtemps qu'il s'agit de problèmes impliquant

des vitesses modérées et des forces qui satisfont suffisamment pour le degré d'exactitude à atteindre, aux principes de la mécanique ancienne, les résultats dans la mécanique réformée ne différeront guère de ceux obtenus jusqu'ici. II en sera autrement dans le cas où, pénétrant dans les mouvements qui se réalisent à l'intérieur des corps jusque dans les atomes, les vitesses deviennent comparables à celle de la lumière.

Je ne vous ai pas parlé jusqu'ici du principe de la conservation de l'énergie. Est-ce à dire que celui-là au moins est resté intact? Tous ceux qui, même de loin, ont suivi les découvertes remarquables de Becquerel, des Curie, de J.-.J. Thomson, Rutherford, Soddy et de tant d'autres, savent que, pendant ces recherches, il paraissait souvent en danger. Pour ne rappeler qu'une chose, un gramme de radium donne constamment, sans qu'on soit en état de constater un changement quel qu'il soit, une énergie d'environ 100 petites calories par heure, c'est-à-dire que 6,5 kg. environ de cette substance énigmatique -— si l'on était en état de se les procurer — fournirait le travail, ordinairement désigné sous le nom d'un «cheval». Quelle est la source mystérieuse de ce travail? C'est là la grave question qu'on s'est posée. Parmi les nombreuses réponses qui ont été données, il y en a une se rattachant à la théorie des électrons qui, dans ces dernières années, a pris le dessus et qui paraît nous donner la clef du mystère.

Cependant, avant de vous donner l'explication de ce phénomène, regardons d'un peu plus près ce qui se passe. Le radium — on l'emploie ordinairement dans sa combinaison avec le chlore ou le brome — émet trois espèces de rayons qu'on désigne sous les noms α, β, y. Les rayons β ne diffèrent des rayons cathodiques que par leur plus grande vitesse; ils se composent d'électrons négatifs, qui se meuvent avec des vitesses différentes allant jusqu'à

95 % de celle de la lumière. Quand on fait agir sur toute la radiation émise une force magnétique d'une certaine intensité, on observe qu'une partie des rayons subit une déviation opposée à celle des rayons ß. Ce sont les rayons α, qui — la déviation le prouve — doivent se composer de petites particules positives. Remarquez bien que je ne dis pas électrons positifs; c'est que ces particules ne sont pas aussi simples. Elles se composent, en effet, de petits noyaux neutres liés à des électrons positifs et elles ont donc une masse apparente beaucoup plus grande. Les rayons γ enfin ne sont pas déviés du tout: ils possèdent toutes les propriétés des rayons Roentgen, c'est-à-dire qu'ils ont surtout une très grande force de pénétration. Mais ce qui les distingue essentiellement des rayons α et β, c'est qu'ils ne contiennent absolument pas d'électrons. Ce sont dans l'éther des ébranlements périodiques brusques, rapidement amortis et produits probablement dans le radium même par le choc des particules α contre les molécules non décomposées. Nous n'en parlons pas ici. Ce qui nous intéresse particulièrement, ce sont les rayons α, composés de particules positives, car Rutherford a démontré que la plus grande partie de l'énergie émise par le radium (probablement plus de 99 %) est transportée par ceux-là.

Il y a un autre fait d'une haute importance. La propriété de la radioactivité n'appartient pas seulement au radium; il y a bien d'autres éléments qui la possèdent. La nature de la radioactivité d'un élément n'est pas seulement une propriété invariable de cet élément, elle peut servir aussi pour distinguer cet élément radioactif d'un autre. Ce moyen est même infiniment plus délicat que la réaction spectroscopique.

Examinons maintenant les résultats des expériences à la lumière de l'explication qu'en donnent MM. Rutherford

et Soddy. L'atome d'une matière ne possède pas seulement un électron négatif et un électron positif; il est tout entier composé d'électrons des deux signes en nombre égal. Pour le radium, l'équilibre de ces électrons est instable. Voici ce qui arrive Supposons, que nous ayons une certaine quantité de radium pur. Pendant la première seconde, une certaine fraction du nombre total des atomes se décompose, se transforme en projetant ces particules positives 8 dont il a été question il y a un instant, et qui forment les rayons α. Dans la seconde suivante, c'est la même fraction du nombre restant d'atomes qui se transforme, et ainsi de suite. Nous en concluons 1° que le radium, se décomposant en un autre élément, doit diminuer, et 2° que le poids atomique du nouvel élément formé sera inférieur à celui du premier, chaque atome décomposé ayant perdu une particule α. Il y a ici une question intéressante qui s'impose. Certains atomes du radium ne vivent tels quels qu'une seconde, d'autres vivent deux secondes, d'autres encore trois secondes, etc.; quelle est la vie moyenne de tous les atomes? Rutherford a déterminé approximativement sa durée par différentes méthodes qui donnent des résultats suffisamment concordants: la vie moyenne des atomes de radium est environ de 1500 à 2000 ans 9.

La nouvelle substance formée par la décomposition du radium est un gaz qui possède toutes les propriétés chimiques d'un élément. A une époque où l'on expliquait autrement ce qui se passe, on lui a donné le nom d'émanation. Cet élément manifeste des propriétés analogues à celles du radium, c'est-à-dire que lui aussi se décompose en donnant un nouvel élément et en projetant des particules électrisées positives; mais tandis que la vie moyenne des atomes du radium, est de 1500 à 2000 ans, celle des atomes de l'émanation n'est que de cinq jours et huit

heures. C'est donc une substance qui se forme lentement, mais qui se décompose rapidement.

Il est utile de faire une remarque sur ce qu'on appelle la vie moyenne des éléments. Cette grandeur est pour chacun des éléments radioactifs une constante qui, dans l'identification de l'élément, rend les mêmes services que le poids atomique dans le cas d'atomes non radioactifs, La vie moyenne de l'émanation — nous venons de le voir — est beaucoup plus petite que celle du radium. L'énergie de la décomposition se dégage donc en moins de temps, et sa radiation est, de ce fait, beaucoup plus intense. La décomposition du nouvel élément qui, lui aussi, est instable, conduit à un troisième, et celui-ci à un quatrième élément. Ce dernier enfin se décompose en un élément stable et connu: l'hélium. L'histoire de cette dernière découverte qu'on doit à MM. Rutherford, Ramsay et Soddy est si curieuse et en même temps si instructive qu'elle mérite d'être étudiée d'un peu plus près. L'hélium est un élément dont on connaît par l'analyse spectroscopique depuis longtemps la présence dans le soleil. En 1895 cependant, sir W. Ramsay réussit à le trouver aussi dans des substances terrestres. C'est un gaz absolument inerte (inactif), se trouvant tel quel à l'état d'occlusion dans certains minerais, qui sont tous radioactifs. Voici le raisonnement que faisaient les phycisiens que je viens de. nommer: L'émanation qui se forme par la décomposition du radium est également un gaz inerte qui, souvent, reste enfermé, c'est-à-dire à l'état d'occlusion, dans les combinaisons de radium dans lesquelles il prend naissance. [La. radiation qu'on observe dans ce cas est la somme des radiations du radium et de l'émanation réunis.] Il est donc possible que l'hélium, qui est renfermé dans certains minerais radioactifs, soit le résultat définitif et stable des décompositions successives du radium et de son émanation,

qui s'y trouvent également. Pour vérifier ce raisonnement, MM. Ramsay et Soddy opéraient dans une de leurs expériences avec 50 milligrammes de bromure de radium. L'émanation qu'ils recueillaient occupait un volume qui était à peine d'un à deux centièmes de millimètre cube. Cette quantité, si petite qu'elle fût, leur suffisait cependant pour l'analyse spectroscopique, qui les conduisait au résultat suivant:

Le spectre de l'émanation change continuellement. Après trois jours, on voit apparaître une des raies caractéristiques. (D3) et peu après le spectre complet de l'hélium. Il est donc démontré par l'expérience que le radium se décompose en hélium et qu'une des formes intermédiaires et transitoires est ce qu'on a appelé l'émanation. On conçoit maintenant sans peine que d'après la théorie des électronistes à outrance, l'énergie émise par le radium doit avoir sa source dans la décomposition ou l'explosion, si vous voulez, d'un certain nombre d'atomes pendant la première seconde, d'autres atomes pendant la seconde suivante, et ainsi de suite. Mais on peut se demander si l'énergie totale des électrons, qui seuls composent l'atome, est assez grande pour expliquer des dégagements d'énergie aussi considérables que ceux que nous constatons dans le cas du radium. Car, nous le savons déjà: l'effet de la décomposition est relativement énorme. Si tous les atomes de l'émanation, par exemple, se décomposent, l'énergie libérée, est de trois à quatre millions de fois plus grande que celle qui se manifeste dans l'explosion d'un volume égal du mélange détonnant d'oxygène et d'hydrogène. Cela s'explique très bien dans la théorie des électronistes. En effet, si l'on calcule l'énergie totale que représente l'ensemble des électrons dans un atome, on arrive à ce résultat qu'elle suffit pour alimenter pendant plus de dix millions d'années le dégagement d'énergie qu'on constate dans le cas du

radium. D'autre part, on a vu que la vie du radium ne dépasse guère quelques milliers d'années. L'énergie manifestée pendant cette période n'est donc que la dix millième partie du stock qu'il possède. Nous pouvons en conclure que les phénomènes si intéressants de la radioactivité ne sont nullement en contradiction avec le principe de la conservation de l'énergie, pourvu qu'on admette que les atomes sont des complexes d'électrons, représentant ensemble une certaine quantité d'énergie de nature électromagnétique. Quant à la cause de la transformation de certains atomes pendant la première, d'autres atomes pendant la seconde unité de temps, etc., nous n'en savons rien pour le moment. Jusqu'à l'instant même de l'explosion, les propriétés physiques et chimiques ne subissent aucun changement. Subitement sans que rien ne le fasse prévoir, l'atome fait explosion en projetant une particule positive. L'énergie, mise en liberté dans cette explosion, est retrouvée en grande partie dans la force vive des particules α. C'est cette force vive qui donne la chaleur lorsque les rayons α sont absorbés; c'est elle qui, dans le choc, brise les molécules des gaz en mettant en liberté leurs électrons négatifs, c'est-à-dire les ionise; c'est elle encore qui sépare les atomes d'hydrogène et d'oxygène dans la décomposition des molécules d'eau 10

Il est vrai que jusqu'ici nous n'avons parlé que du radium; il suffit d'ajouter que, qualitativement, les propriétés des autres substances radioactives sont absolument les mêmes. Dans le cas du thorium, par exemple, on constate également une série de décompositions successives. Dans toutes —peut-être à une exception près — des particules positives sont projetées. Cette décomposition cependant se fait d'une manière si lente, la vie moyenne est si longue, la radiation qui l'accompagne est si petite, que, dans cet élément, connu depuis bien longtemps, elIe

a pu échapper aux physiciens. Il en est de même pour l'uranium.

Mais ici deux questions se posent. D'abord: la radioactivité appartient-elle seulement aux éléments que nous venons de nommer ou est-elle commune à tous les éléments? et secondement: Comment se fait-il que le radium, dont la durée est relativement restreinte, ne soit pas encore épuisé? A la première question, certains physiciens répondent que tous les éléments sont plus ou moins radioactifs et que ceux qui, actuellement, sont considérés comme stables, ne nous paraissent tels que parce que la transformation se fait d'une manière extrêmement lente. Ceci n'est pas l'opinion de tous les physiciens. Soddy, par exemple, est d'avis que la radioactivité n'appartient qu'à quelques éléments; si, dans les autres, des transformations se produisent, celles-ci ne sont pas accompagnées dc la projection de particules α.

Quant à la seconde question: Comment se fait-il que le stock du radium ne soit pas encore épuisé? Voici la réponse que la théorie (de la désagrégation) en donne. L'activité de l'uranium est un million de fois plus faible que celle du radium, sa vie est donc un million de fois plus longue. Cet élément se décompose en projetant une particule α et en formant un autre élément, très éphémère celui-là, qui se décompose à son tour, etc. Dans cette série de transformations successives, un des termes serait le radium, de sorte que la quantité de cet élément qui disparaît serait remplacée — en partie ou en entier — par une nouvelle quantité formée par la décomposition de l'uranium.

Ajoutons, pour être plus complet, que, d'après la même théorie, le polonium ne serait qu'un dérivé du radium comme celui-ci lui-même est un dérivé de l'uranium. Enfin, que la particule α ne serait autre chose que l'atome de l'hélium 11.

Ici les preuves expérimentales cependant deviennent beaucoup plus rares. Nous quittons donc ce domaine pour résumer brièvement les principales conséquences de la théorie électroniste pour la chimie. D'abord nous savons que les électrons sont beaucoup plus petits que les atomes qui, jusqu'à présent, étaient considérés comme formant la limite de la divisibilité chimique. Il y a plus: dans le radium, comme dans toute autre substance radioactive, à chaque moment un certain nombre d'atomes sont sur le point d'éclater, tandis que les autres sont stables. Il y a donc une différence entre les atomes du même élément. qui, jusqu'ici, furent considérés comme identiques. Enfin, les recherches sur la radioactivité ont fait voir que certains éléments — sans qu'on soit en état de l'empêcher ou de l'accélérer — se décomposent spontanément en formant d'autres éléments, ce qui — il est inutile de le dire — était considéré jusqu'ici comme impossible 12.

Je termine. La théorie des électrons a fait en peu d'années des progrès immenses. Dans sa marche à travers le domaine des sciences physiques, elle a renversé des notions et des lois qui paraissaient parmi les plus solides et les mieux fondées. Pour le moment, il y a des ruines, mais nous avons la certitude que bientôt, de ces ruines, s'élèveront les, nouvelles constructions, plus belles, plus vastes et plus solides.

NOTES

1 Si l'oscillation se fait suivant AB, il se propagedans toute direction y perpendiculaire à AB, avec une vitesse égale à celle de la lumière, une onde électrique (variation périodique de la force électrique), qui est dans le plan passant par y et AB, et une onde magnétique (variation périodique de la force magnétique) passant par y et normale à AB.

2 Soit OXYZ un système de coordonnées rectangulaires droit. Un électron, de masse m et de charge + e, se meut avec une vitesse y dans la direction OX. Soumis à l'action d'une force électrique constante E selon OY, l'électron décrit dans le plan OXY une parabole, dont OX est la tangente au sommet, absolument comme un corps lancé avec une vitesse horizontale décrit une parabole sous l'influence de la force constante, qui est la pesanteur. Au sommet, la force normale (selon OY) est eE, l'accélération normale est donc eE : m; d'autre part, cette accélération normale est v 2 : r 1 , si r 1 est le rayon de courbure; on a donc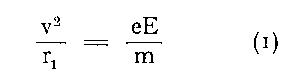

Soumis à un champ magnétique constant H selon OY, l'électron éprouve une force evH selon OZ, donc normale à sa vitesse. Cette force restera normale à la vitesse, et à H; il s'ensuit que sous son influence la trajectoire décrite dans le plan OYZ est un cercle, tangent en O à l'axe OX. La force normale en O est evH, l'accélération normale evH : m, et l'on a donc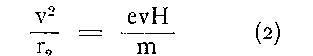

si r 2 est le rayon du cercle. Des équations (1) et (2) on tire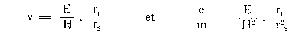

de sorte qu'en mesurant E, H, r 1 et r 2 on peut calculer la vitesse v et le rapport entre la charge e et la masse m d'un électron. En procédant d'une manière analogue, on a trouvé pour e : m environ 3 x 10, la charge étant exprimée en unités électrostatiques C. G. S. Les vitesses trouvées sont très différentes; celle des rayons cathodiques ordinaires est d'environ 0,1 de celle de la lumière.

Si l'on augmente un volume rempli de vapeur d'eau saturante subitement dans la proportion de 1 à 1,25, la vapeur ne se condense pas malgré l'abaissement de température, si l'air est absolument pur. Mais si cet air pur est ionisé, c'est-à-dire si l'on y a produit des électrons libres, tous les électrons négatifs, et seulement ceux-là, deviennent des centres de gouttelettes. Supposons que le nombre des gouttelettes formées soit n, et que e' soit la quantité totale d'électricité qu'elles contiennent; dans ce cas, la charge e de chaque gouttelette, c'est-à-dire de chaque électron sera e' : m.

On mesure facilement la charge totale e' de toutes les gouttelettes. Leur nombre se déduit de la manière suivante. Il existe une relation connue entre la vitesse avec laquelle elles tombent et leur rayon, de sorte qu'en mesurant cette vitesse, on connaît le rayon, donc aussi le poids de chaque gouttelette.

Comme leur poids total, celui de l'eau formée, et connu, on obtient le nombre par une simple division.

En procédant ainsi, J.-J. Thomson et H. A. Wilson trouvent la 10 charge e d'un électron égale à 3,4 X 10 unités-électrostatiques C. G. S. Celle d'un ion d'hydrogène dans l'électrolyse est la même, mais le rapport e : m y est 2000 fois plus petit. Il s'ensuit que la masse d'un ion ou d'un atome d'hydrogène est d'environ 2000 fois plus grande que celle d'un électron.

3 Dans deux métaux différents, les électrons négatifs ne se séparent pas de l'atome avec la même facilité. Les atomes exercent donc sur ces électrons des attractions différentes, et si ces deux métaux sont en contact, les électrons négatifs libres seront attirés davantage par un des métaux A que par l'autre B. Il en résulte que le premier aura, par rapport au second, un certain potentiel négatif. C'est d'une manière analogue qu'il faut s'expliquer la différence de potentiel ou la force électromotrice d'une pile galvanique.

4 C'est par l'intermédiaire des électrons négatifs que la combinaison chimique se fait entre des atomes différents. L'électron négatif dans un atome Na étant retenu par une force inférieure à celle qui retient l'électron négatif dans un atome Cl, on doit, d'après les électronistes, concevoir

NaCI comme se formant par l'attraction de l'atome Cl sur l'électron négatif de l'atome Na, ce qui peut se représenter par le schéma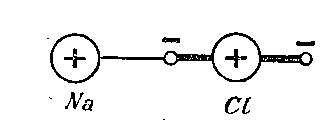 c'est-à-dire
des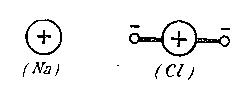 ions positifs (Na) et des ions négatifs (Cl).

Lorsque cette solution fait partie du circuit d'un courant électrique, la force électromotrice pousse d'abord l'ion (Cl) dans la direction de l'anode A et l'ion (Na) dans celle de la cathode C; puis, elle fait sortir à la cathode un électron négatif qui, en se liant à l'ion positif (Na), en fait un atome neutre Na. L'ion négatif (Cl), par contre, cède son électron négatif superflu à l'anode et revient ainsi également à l'état d'atome neutre Cl.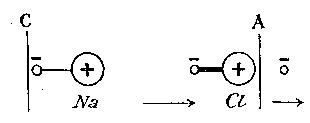

sur chaque électron négatif (voir note 2) une force evH qui le pousse dans la direction a 2 a 4. Le potentiel dans un point de a 4 deviendra donc inférieur à celui du point correspondant de a 2, ce qui crée, pour les électrons négatifs, une force électrique E dans la direction a 4 a 2. Lorsqu'il y a équilibre, les deux forces opposées evH et eE sont égales, ce qui permet de calculer la vitesse v = E : H avec laquelle les électrons libres se meuvent dans le métal. Il se trouve que cette vitesse est très petite comparée à celle du mouvement désordonné qui correspond à la température. Dans certains métaux (fer, zinc), le potentiel ne s'abaisse pas en a 4, mais en a 2, ce qui indiquerait un mouvement d'électrons libres ayant une charge positive. Lorentz croit cependant à la possibilité d'expliquer cette forme du phénomène de Hall en admettant à côté des électrons libres négatifs une certaine mobilité limitée des électrons positifs dans les atomes.

6 Soumettons un rayon cathodique simultanément à l'action d'un champ électrique et d'un champ magnétique de la manière indiquée dans la note 2. Dans ce cas, les électrons viendront impressionner la plaque photographique posée parallèlement au plan YOZ à la distance x 0, en un point dont les coordonnées y et z se trouvent par le raisonnement suivant. Si la courbure dans le plan XOY pour le point O est grande, la déviation de l'axe OX, c'est-à-dire l'ordonnée y le sera également. On peut dire qu'en première approximation les y et z sont proportionnels aux courbures (voir note 2).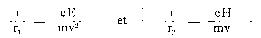

En éliminant y on trouve donc, C étant une constante, une parabole y == Cmz 2 si la masse totale ni est invariable. La courbe obtenue sur la plaque photographique n'est pas une parabole; il s'ensuit que ni est variable et les différences entre les ordonnées des deux courbes prouvent 1° que la masse totale, qui se compose de la masse réelle m 0 et la masse apparente m 1 augmente avec la vitesse, et 2° que le rapport entre les masses totales correspondant aux vitesses v et v' est le même que celui entre les masses apparentes m 1 et m 1 '. On a donc (m 0 +m 1 ). (m 0 +m 1 ')= m 1 : m 1 ', c'est-à-dire m 0 = o.

7 Lorsqu'un corps commence à émettre de la lumière dans une certaine direction, la quantité de mouvement électromagnétique du milieu augmente d'autant que la quantité du mouvement mécanique du corps diminue. II s'exerce donc sur le corps une certaine actions.

La quantité de mouvement électromagnétique se propage dans la direction du rayon et se transforme de nouveau en quantité de mouvement mécanique, lorsqu'après un certain temps la lumière est absorbée par un autre corps. A ce moment seulement il s'exerce sur le corps absorbant (à surface noire) une réaction ou pression, qui, étant numériquement égale à la densité de l'énergie de l'onde, peut être facilement calculée. Elle a été mesurée par Lebedew (Ann. der Phys. 6, S. 433. 1901) et Nicholls et Hull (Ann. der Phys. 12, S. 225. 1903).

8 Soddy (Jahrbuch der Radioaktivität und Elektronik 2, S. 1-4. 1905) croit que les particules projetées par les atomes en décomposition sont neutres au moment de l'explosion. Se mouvant dans un gaz, elles ionisent le gaz comme elles s'ionisent elles-mêmes; c'est-à-dire que par les chocs elles perdent leur électron négatif, comme elles le font perdre à certains atomes du gaz.

9 Sur le nombre x d'atomes non décomposés à l'instant t, il y aura λxdt, qui feront explosion pendant le temps dt, si la fraction λ indique la probabilité pour que les électrons dans un atome aient les positions et les vitesses correspondant à l'état d'explosion. D'autre part, la diminution du nombre des atomes non décomposés pouvant s'écrire — dx, nous avons —dx = λxdt ou x = ae -λt si a est e nombre initial d'atomes.

Les degrés de radioactivité J 0 et J t correspondant aux instants o et t sont proportionnels aux nombres des atomes en décomposition λ adt et λxdt, c'est-à-dire à a et x. Nous en concluons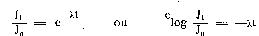

Pour l'émanation du thorium, l'activité devient la moitié de sa valeur initiale après environ 60 secondes. Il s'ensuit

Le coefficient λ, que nous venons d'introduire, est «la constante de la radioactivité».

Le nombre des atomes décomposés pendant la période de t à t +dt est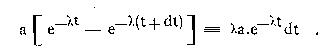

Leur vie étant de t unités de temps, on trouve comme vie moyenne de tous les atomes a: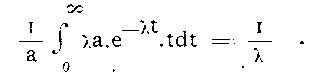

La vie moyenne est donc la valeur réciproque de la constante de la radioactivité λ. Pour l'émanation du thorium, on trouve ainsi 87 secondes.

10 Au mois de juin 1905, M. John Butler Burke annonçait qu'ayant saupoudré de traces de bromure de radium un bouillon stérilisé à demi-solidifié par l'addition de gélatine, il avait obtenu des cultures offrant toutes les apparences de la vie. Sir W. Ramsay croit pouvoir expliquer le phénomène observé de la manière suivante (Revue générale des Sciences pures et appliquées, septembre 1905): Les grains de radium, en s'enfonçant un peu au-dessous de la surface, décomposent l'eau et ils se forment des bulles microscopiques, remplies d'oxygène, d'hydrogène et d'émanation. Par la propriété connue, mais non expliquée, de l'émanation de coaguler l'albumine, il se forme autour de chacune de ces bulles une membrane qui lui donne l'aspect d'une cellule. L'émanation enfermée continue à décomposer l'eau, la bulle éclate. Les gaz s'échappant par les crevasses, entraînent un peu d'émanation, et le phénomène recommence. Sur la première bulle, ressemblant à une cellule de levure, se forme une seconde ressemblant à un bourgeon. La seconde bulle se comporte comme la première, et le phénomène se répète aussi longtemps que le radium engendre de l'émanation, c'est-à-dire pendant des milliers d'années.

11 Toutes ces hypothèses semblent être confirmées par les dernières expériences de Boltwood (Phil. Mag. (6)9. 1905), Soddy (Phil. Mag. 9. 1905) et Strutt (Chemical News 91. 1905).

12 Les mémoires importants relatifs à la théorie des électrons se trouvent réimprimés ou résumés dans H. Abraham et P. Langevin: Les quantités élémentaires d'électricité, ions, électrons, corpuscules, 2 vol. in-8°; Paris, Gauthier-Villars, 1905.

La théorie mathématique complète se trouve dans la Theorie der Elektrizität de MM. A. Föppl et M. Abraham. (Tome I, Einführung in die Maxwell'sche Theorie, par A. Föppl.) (Tome II, Elektro-magnetische Theorie der Strahlung). Teubner, Leipzig.

La théorie de la désagrégation est exposée par Frederick Soddy dans un livre dont la traduction allemande porte le titre: die Radioaktivität vom Standpunkte der Desagregationstheorie, Barth, Leipzig.